Initial unemployment claims data came out today and
weekly unemployment claims decreased to 415,000. The number has bounced around quite a bit recently causing some gyrations in the market and I thought it would be instructive to dig down a little further into the data.
One item to note from this first graph is how volatile the raw data is. Note how around year end the unemployment claims spike up dramatically. Compare the raw data to the 4 week moving average seasonally adjusted data and you can understand why the claims data has bounced around so much recently; we are in the post holiday layoff period.

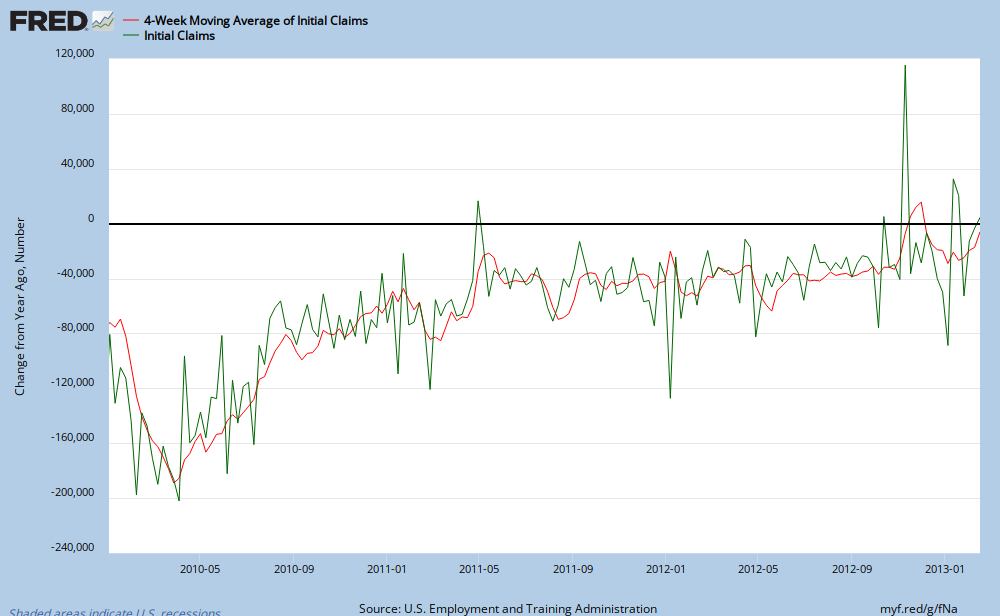
Next let us examine the year over year change in initial claims. What is actually impressive to me is how close the raw data and 4 week seasonal data track each other. (Note these two graphs do not show today's data) I have drawn in some black lines showing the rise starting in 2008, a peak in early March 2009 and then a bottom and rebound in early 2010. Note this is the change in claims and as you can see we are still dropping on a year over year basis but the rapid fall in initial claims has ended and we are trending back towards zero. You can also see the most recent raw claims data is bouncing around quite a bit, again due to seasonal affects and possibly the weather.
Is the glass half empty or half full?
We can torture the data a bit further and just for fun and see what models predict will happen next. Using March 27, 2010 as the baseline (the peak in the rate of decline in initial claims) I let excel extrapolate the data out another 15 weeks. Bottom line is you can come up with either a positive or negative prediction depending upon how may polynomials you use.
Using a 2 polynomial regression predicts (R2 of .9712) claims are near their deceleration point and will then continue to keep dropping over time.
You want a bearish case? No problem! Using a 5 polynomial (R2 of .9763) regression initial unemployment claims will eventually reverse their fall in 12 weeks or so and start to rise on a year over year basis